ChatGPTが大バズリしている昨今です。僕はプロンプトを考えるのが面倒なので（ええ…)あまり使わないのですが、友人が論文を書くのに使っていたり、僕の母親が話し相手に使っていたりするようです。親不孝な息子でごめんなさいという感じもします。 ところで、ChatGPTのような言語生成モデルでしばしば利用されているのが、Transformerと呼ばれるニューラルネットワークの構成です。Transformerでは、Multihead Attentionと呼ばれるレイヤーを入力のトークン列に対し繰り返し適用し複雑なモデルを構成します。このブログでは、その簡略版である1レイヤーのAttention(Multiheadではない)に着目し、これが何をしているのかを勉強し、ついでにコードを書いて動かしてみます。
Attentionは、入力としてトークンの列が与えられることを仮定しているので、まずトークン列をネットワークに入力するために前処理します。
トークン列というのは文字通りトークンからなる列のことです。トークンは有限集合の要素です。実用上はbyte pair encodingにより得られた部分文字列などがこれに該当しますが、とりあえず気にしなくていいです。トークンの集合を\(V\)とし、\([Nv] := {1, ..., Nv}\)と番号付けしておきます。トークン列を\(x = x[1: l]\)と書きます。また、トークン列の最大の長さを\(L\)とします。トークンとして連続値や無限集合は扱えないと思いますが、素人なので何か抜け道があるかどうかは知りません。
適当な\(d_e \times Nv\)次元の行列\(W_e\)を使って、\(v\)番目のトークンから埋め込み（Token embedding）を \(e = W_e[:, v]\)により得ます。これは\(d_e\)次元のベクトルになります。なお、numpy風に\(i\)番目の行ベクトルを\(W[i, :]\)、\(j\)番目の列ベクトルを\(W[:, j]\)と書いています。この行列\(W_e\)は勾配降下により学習されるようです。
適当な\(d_p \times L\)次元の行列\(W_p\)を使って、トークン列中の\(l\)番目にトークンがあるという情報から、位置埋め込み（Positional embedding）を \(p = W_p[:, l]\)により得ます。これも\(d_e\)次元のベクトルになります。正直なんの意味があるのかよくわからないのですが、これを先程のトークン埋め込みに足してトークン列\(x\)の\(t\)番目のトークン\(x[t]\)に対する埋め込みを\(e = W_e[:, x[t]] + W_p[:, t]\)によって得ます。これ足して大丈夫なのかな？って思うんですが。 位置埋め込みは、学習されることもあるようですが、Transformerが最初に提案されたAttention Is All You Needの論文では、以下のように構成されています。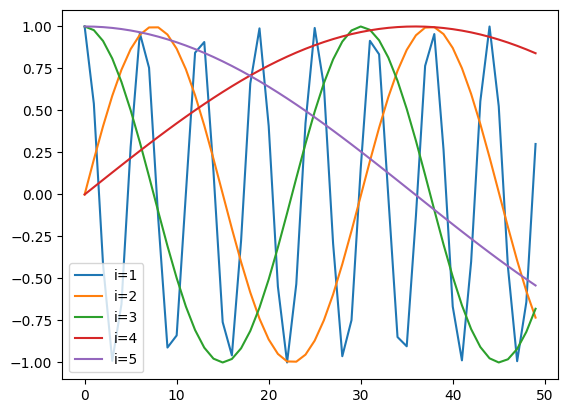 \[ \begin{align*} W_p[2i - 1, t] &= \sin (\frac{t}{L^{2i / d_e}}) \\ W_p[2i, t] &= \cos (\frac{t}{L^{2i / d_e}}) \\ &~~~~~(0 < 2i \leq d_e) \end{align*} \] これを\(L=50, d_e = 5\)として可視化してみましょう。
import matplotlib
import numpy as np
from matplotlib import pyplot as plt
matplotlib.font_manager.fontManager.addfont("NotoEmoji-Medium.ttf")
L = 50
d_e = 5
x = np.arange(L)
for i in range(1, 1 + d_e):
if i % 2 == 0:
w_p = np.sin(x / L ** (i / d_e))
else:
w_p = np.cos(x / L ** ((i - 1) / d_e))
_ = plt.plot(x, w_p, label=f"i={i}")
plt.legend()<matplotlib.legend.Legend at 0x7f0d6b51bdf0>
というわけで、この埋めこみは各成分ごとに異なる周波数での単語を埋め込むようです。これにより、短いコンテキストの中での位置も同時に考慮できるのかな。
Transformerの主要な構成要素になるのがSelf-Attentionです。Self-Attentionでは、入力されたトークン列中のすべてのトークンの組み合わせについて、そいつらの組み合わせがどれくらい重要なのかというモデル化を行います。具体的に、単一クエリに対するAttentionでは、現在のトークンから得た埋め込み\(e_t\)と\(x\)中のすべてのトークンの埋め込み\(e_0, e_1, ..., e_{Nv} \in E\)に対し、以下のような操作を行います。 \[ \begin{align*} q_t &\leftarrow W_q e_t + b_q \\ k_{t'} &\leftarrow W_k e_{t'} + b_k,~\forall e_{t'} \in E \\ v_{t'} &\leftarrow W_v e_{t'} + b_v,~\forall e_{t'} \in E \\ \alpha_{t'} &\leftarrow \frac{\exp(q_t^\top k_{t'} / \sqrt{d_{\textrm{attn}}})}{\sum_u \exp(q_t^\top k_{t'} / \sqrt{d_{\textrm{attn}}})},~\forall e_{t'} \in E \\ v_\textrm{attr} &\leftarrow \sum_{t = 1}^T \alpha_{t'} v_{t'} \end{align*} \] 埋め込みの次元を\(d_\textrm{in}\)、出力の次元と\(d_\textrm{out}\)とすると、\(W_q, Q_k\)は\(d_\textrm{attn} \times e\)の行列、\(W_q, Q_k\)は\(d_\textrm{out} \times d_\textrm{in}\)の行列、\(b_*\)はベクトル（バイアス項）です。ここで、\(q^\top k_{t'}\)の値でソフトマックスをとって\(v\)にマスクをかけるので、これは現在のトークンと\(t'\)番目のトークンが「どれくらい対応しているか」を表していてほしいです。\(v_{t'}\)が何を表しているかはタスクによって異なると思いますが、\(t'\)番目のトークンの埋め込みに線形に関係する値が入っているはずです。このトークン列に後ろ向きの因果関係がない場合（あるトークン\(x[t]\)が、任意の未来のトークン\(x[t']~\textrm{where}~t < t'\)に依存しない場合）は、\(\alpha_{t'}\)にマスクをかける(\(\alpha_{t'}[i] = 0 ~\textrm{if}~t < i\))こともあります。なので、未来を予測する際にはこのマスクをかけるのが一般的なようです。
実際に、時系列から何か（次の単語、ラベルなど）を予測する際には、この単一クエリに対するAttentionを長さ\(T\)の系列内のすべてのトークンに対して計算し、\(d_\textrm{out} \times T\)の行列\(\tilde{V}\)を得ます。
とりあえずこれを学習させてみましょう。今回はjaxとequinoxを使ってモデルを書いてみます。
import equinox as eqx
import jax
import jax.numpy as jnp
class Attention(eqx.Module):
w_q: jax.Array
b_q: jax.Array
w_k: jax.Array
b_k: jax.Array
w_v: jax.Array
b_v: jax.Array
sqrt_d_attn: float
def __init__(self, d_in: int, d_attn: int, d_out: int, key: jax.Array) -> None:
wq_key, bq_key, wk_key, bk_key, wv_key, bv_key = jax.random.split(key, 6)
self.w_q = jax.random.normal(wq_key, (d_attn, d_in))
self.b_q = jax.random.normal(bq_key, (d_attn, 1))
self.w_k = jax.random.normal(wk_key, (d_attn, d_in))
self.b_k = jax.random.normal(bk_key, (d_attn, 1))
self.w_v = jax.random.normal(wv_key, (d_out, d_in))
self.b_v = jax.random.normal(bv_key, (d_out, 1))
self.sqrt_d_attn = float(np.sqrt(d_attn))
def __call__(self, e: jax.Array) -> jax.Array:
"""Take a matrix e with shape [d_in x seq_len], compute attention for all tokens in e.
Outputs a matrix with shape [d_out x seq_len]
"""
q = self.w_q @ e + self.b_q
k = self.w_k @ e + self.b_k
v = self.w_v @ e + self.b_v
alpha = jax.nn.softmax(q.T @ k / self.sqrt_d_attn, axis=-1)
return v @ alpha.T
def causal_mask(x: jax.Array, fill: jax.Array = -jnp.inf) -> jax.Array:
ltri = jnp.tri(x.shape[0], dtype=bool, k=-1)
return jax.lax.select(ltri, jnp.ones_like(x) * fill, x)
class MaskedAttention(Attention):
def __call__(self, e: jax.Array) -> jax.Array:
q = self.w_q @ e + self.b_q
k = self.w_k @ e + self.b_k
v = self.w_v @ e + self.b_v
score = causal_mask(q.T @ k) / self.sqrt_d_attn
alpha = jax.nn.softmax(score, axis=-1)
return v @ alpha.Tこれを学習させてみましょう。トークンとして、天気🌧️・☁️・☀️を考えます。この3つの記号に対し適当な埋め込みを与えて、次の日の天気を学習させてみます。一般的にTransformerで用いられる方法とは全く違いますが、なるべく簡単なネットワークで学習できるように、以下のような要素数4のベクトルを埋め込みとします。
最大文字列長は20にします。
WEATHERS = ["🌧️", "☁️", "☀️"]
MAX_SEQ_LEN = 20
def get_embedding(seq: str) -> np.ndarray:
length = len(seq) // 2
e = np.zeros((4, length))
for i in range(length):
w = seq[i * 2: i * 2 + 2]
e[WEATHERS.index(w), i] = 1.0
e[3, i] = (i + 1) / MAX_SEQ_LEN
return eまず簡単なモデルで天気を生成してみます。次の日の天気は、前の日の天気にもとづいて確率的に決まることにしましょう。🌧️・☁️・☀️がマルチバイト文字であることに注意して、以下のように実装します。
import dataclasses
_GEN = np.random.Generator(np.random.PCG64(20230508))
_MARKOV = {
"": [0.3, 0.4, 0.3],
"🌧️": [0.6, 0.3, 0.1],
"☁️": [0.3, 0.4, 0.3],
"☀️": [0.2, 0.3, 0.5],
}
def markov(prev: str) -> str:
prob = _MARKOV[prev[-2:]]
return prev + _GEN.choice(WEATHERS, p=prob)
def generate(f, n: int, init: str = ""):
value = init
for _ in range(n):
value = f(value)
return value
@dataclasses.dataclass
class Dataset:
weathers: list[str]
embeddings: jax.Array
next_weather_indices: jax.Array
def __len__(self) -> int:
return len(self.weathers)
def make_dataset(f, seq_len, size) -> Dataset:
w_list, e_list, nw_list = [], [], []
for _ in range(size):
weathers = generate(f, seq_len + 1)
e = jnp.array(get_embedding(weathers[:-2]))
w_list.append(weathers)
e_list.append(e)
nw_list.append(WEATHERS.index(weathers[-2:]))
return Dataset(w_list, jnp.stack(e_list), jnp.array(nw_list))
generated = generate(markov, 10)
generated, get_embedding(generated)('🌧️🌧️🌧️☀️🌧️☁️🌧️🌧️☀️☀️',
array([[1. , 1. , 1. , 0. , 1. , 0. , 1. , 1. , 0. , 0. ],
[0. , 0. , 0. , 0. , 0. , 1. , 0. , 0. , 0. , 0. ],
[0. , 0. , 0. , 1. , 0. , 0. , 0. , 0. , 1. , 1. ],
[0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 ]]))こんな感じです。いま、次の日の天気だけ予測したいので、モデルの出力は集合{🌧️・☁️・☀️}上での確率分布が適切でしょう。Attentionは長さ\(T\)の埋め込み列に対して長さ\(d_\textrm{out} \times T\)の行列をかえします。なので、\(d_\textrm{out} = 3\)とし、Attentionの出力\(\tilde{V}\)に対してソフトマックス関数を適用し、\(P_t = \textrm{softmax}(\tilde{V}[:, t])\)とします。このとき、\(P_t\)の各要素が次の日🌧️・☁️・☀️になる確率を表すとして、モデル化します。これを、対数尤度の和\(\sum_t \log P_t(\textrm{next weather})\)を最大化するように学習しましょう。学習のコードを定義します。
from typing import Callable
import optax
def attn_neglogp(model: eqx.Module, seq: jax.Array, next_w: jax.Array) -> jax.Array:
batch_size = seq.shape[0]
tilde_v = jax.vmap(model)(seq) # B x OUT x SEQ_LEN
logp = jax.nn.log_softmax(tilde_v, axis=1) # B x OUT x SEQ_LEN
logp_masked = logp * jax.nn.one_hot(next_w, num_classes=3).reshape(-1, 3, 1)
return -jnp.mean(jnp.sum(logp_masked.reshape(batch_size, -1), axis=-1))
def train(
n_total_epochs: int,
minibatch_size: int,
model: eqx.Module,
ds: Dataset,
test_ds: Dataset,
key: jax.Array,
learning_rate: float = 1e-2,
loss_fn: Callable[[eqx.Module, jax.Array, jax.Array], jax.Array] = attn_neglogp,
) -> tuple[eqx.Module, jax.Array, list[float], list[float]]:
n_data = len(ds)
optim = optax.adam(learning_rate)
@eqx.filter_jit
def train_1step(
model: eqx.Module,
seq: jax.Array,
next_w: jax.Array,
opt_state: optax.OptState,
) -> tuple[jax.Array, eqx.Module, optax.OptState]:
loss, grads = eqx.filter_value_and_grad(loss_fn)(model, seq, next_w)
updates, opt_state = optim.update(grads, opt_state)
model = eqx.apply_updates(model, updates)
return loss, model, opt_state
opt_state = optim.init(model)
n_optim_epochs = n_data // minibatch_size
loss_list, eval_list = [], []
for epoch in range(n_total_epochs // n_optim_epochs):
key, perm_key = jax.random.split(key)
indices = jax.random.permutation(perm_key, n_data, independent=True)
for _ in range(n_optim_epochs):
e = ds.embeddings[indices]
next_w = ds.next_weather_indices[indices]
loss, model, opt_state = train_1step(model, e, next_w, opt_state)
loss_list.append(loss.item())
test_loss = jax.jit(loss_fn)(
model,
test_ds.embeddings,
test_ds.next_weather_indices,
)
eval_list.append(test_loss.item())
return model, key, loss_list, eval_listこれを実際に走らせてみます。適当に、Attentionの次元を6、天気列の長さを10にします。
D_ATTN = 6
SEQ_LEN = 10
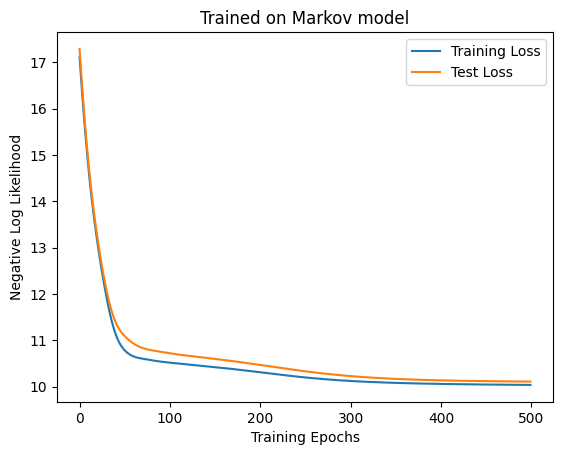
key = jax.random.PRNGKey(1234)
model = MaskedAttention(4, D_ATTN, 3, key)
ds = make_dataset(markov, SEQ_LEN, 1000)
test_ds = make_dataset(markov, SEQ_LEN, 1000)
model, key, loss_list, eval_list = train(500, 100, model, ds, test_ds, key, 1e-2)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on Markov model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
@jax.jit
def accuracy(model: eqx.Module, seq: jax.Array, next_w: jax.Array) -> float:
tilde_v = jax.vmap(model)(seq) # B x OUT x SEQ_LEN
inferred = jnp.argmax(tilde_v[:, :, 0], axis=1)
n_correct = jnp.sum(inferred == next_w)
return n_correct / seq.shape[0]
f"Accuracy: {accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.49800002574920654'
100エポックあたりでロスが落ちなくなっているので収束はしていそうです。実際に何を学習したのか確認してみましょう。とりあえず天気を生成してみます。こんなもの見ても何もわからないのですが、生成の流れを確認しておくにはいいかなと。ビームサーチが使われることが多いようですが、面倒なので今回はもっと簡単な方法を使います。☁️からスタートして、カテゴリカル分布から次の天気をサンプルし、どんどん足していくことにします。
def generate_from_model(
model: eqx.Module,
key: jax.Array,
seq_len: int,
init: str = "☁️",
) -> tuple[str, jax.Array]:
@jax.jit
def step(
model: eqx.Module,
seq: jax.Array,
key: jax.Array,
) -> tuple[jax.Array, jax.Array]:
sample_key, key = jax.random.split(key)
tilde_v = model(seq) # 3 x len(seq)
sampled = jax.random.categorical(key=sample_key, logits=tilde_v[:, 0])
return sampled, key
generated = init
for _ in range(seq_len):
next_w, key = step(model, get_embedding(generated), key)
generated += WEATHERS[next_w.item()]
return generated, key
generated, key = generate_from_model(model, key, 20)
generated'☁️🌧️🌧️☀️🌧️☁️🌧️☀️☀️☀️☁️☁️☀️☀️☀️☀️☀️☁️☁️☀️☁️'こんな感じになりました。当たり前ですがこれを見たところで何もわからないですね。次に、テストデータ中の適当なデータに対しAttentionの中身を可視化してみます。
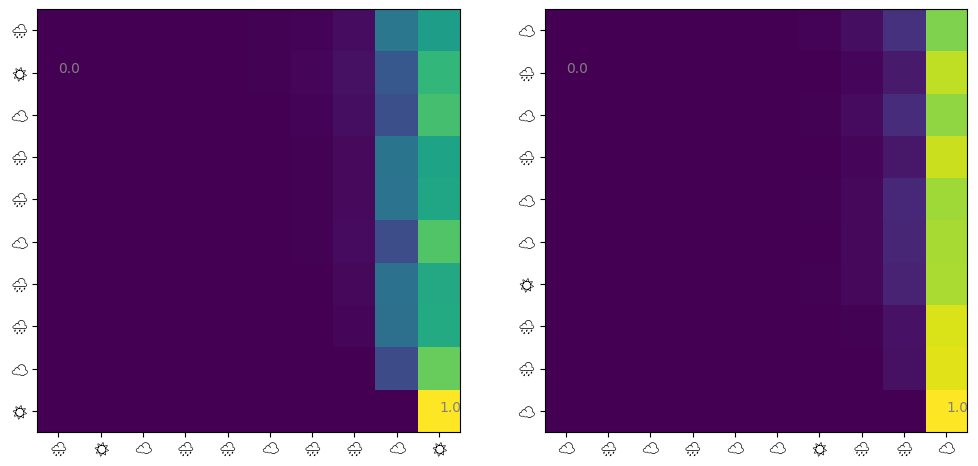
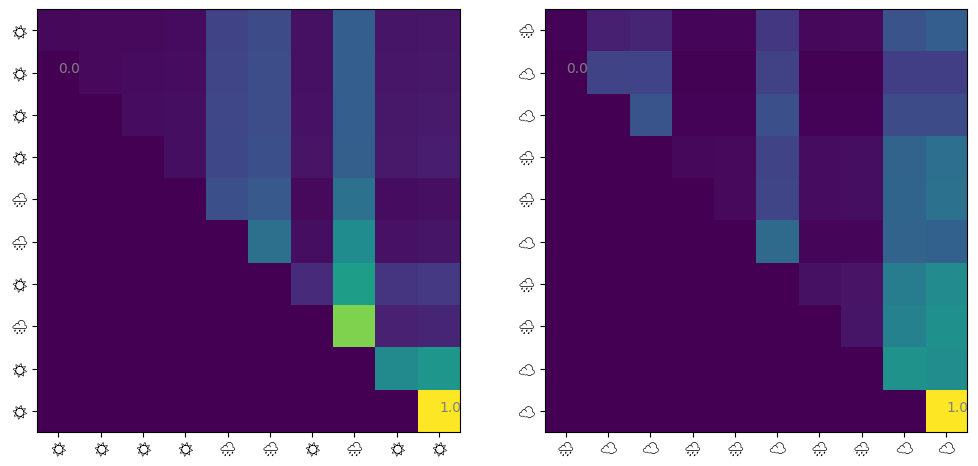
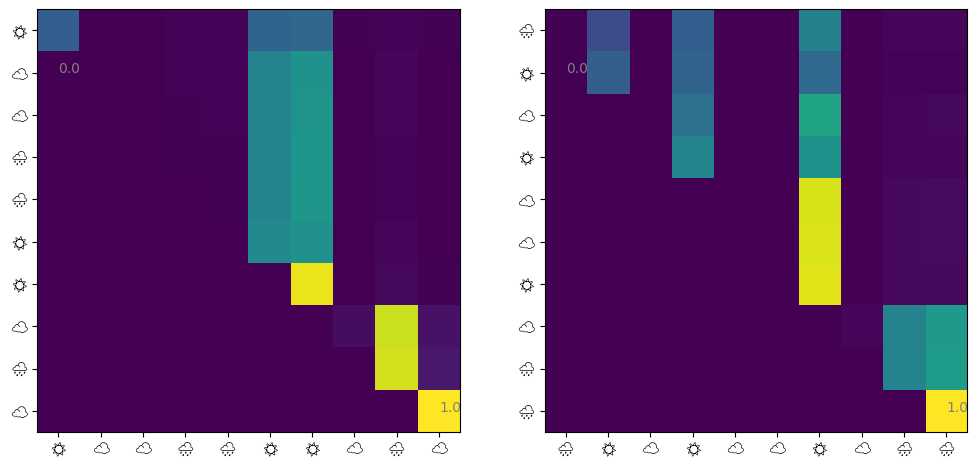
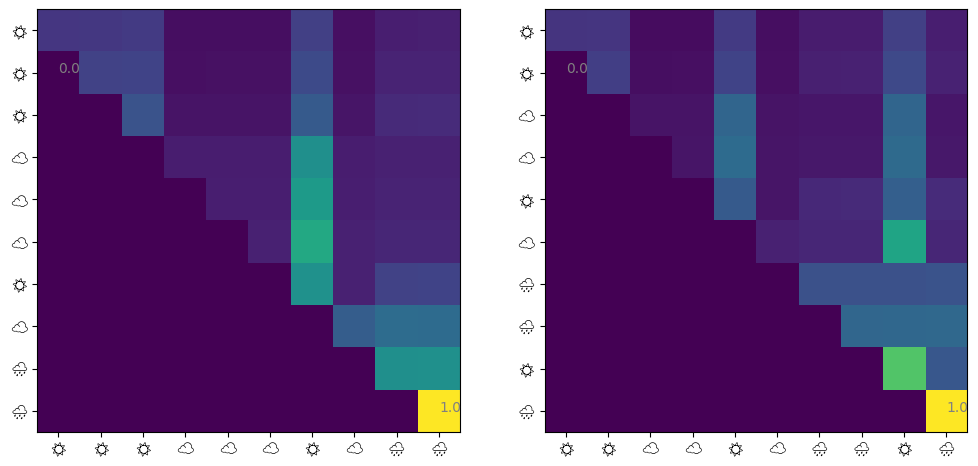
@jax.jit
def get_attn(model: eqx.Module, seq: jax.Array) -> jax.Array:
q = model.w_q @ seq + model.b_q
k = model.w_k @ seq + model.b_k
score = causal_mask(q.T @ k) / model.sqrt_d_attn
return jax.nn.softmax(score, axis=-1)
def visualize_attn(ax, model: eqx.Module, ds: Dataset, index: int = 0) -> None:
attn = np.array(get_attn(model, ds.embeddings[index]))
im = ax.imshow(attn)
ax.set_xticks(
np.arange(10),
labels=[ds.weathers[index][i * 2] for i in range(10)],
fontname="Noto Emoji",
)
ax.set_yticks(
np.arange(10),
labels=[ds.weathers[index][i * 2] for i in range(10)],
fontname="Noto Emoji",
)
for i in [np.argmin(attn), np.argmax(attn)]:
# Show min and max values
im.axes.text(i % 10, i // 10, f"{attn.flatten()[i]:.1f}", color="gray")
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))
visualize_attn(ax1, model, test_ds, 1)
visualize_attn(ax2, model, test_ds, 2)
matplotlibでカラー絵文字が使えなかったのでモノクロの絵文字にしました。というわけで、 1. 直前の天気→直前の天気 のAttentionが最も大きい 2. 他の日の天気→直前の天気 のAttentionも大きい 3. 他はほとんど関係ない
といったことがわかります。マルコフモデルから生成した天気列を学習させたので、1は当たり前ですよね。2の他の日の天気→直前の天気の関係も実際はいらないのですが、注意されているようです。
次に、もう少し複雑なデータを学習させてみましょう。今度は、以下のような方法で11日ぶんの天気を生成します。 1. 1日目、4日目、8日目の天気を独立に生成する 2. 2,3日目の天気を1日目の天気を初期状態とするマルコフ連鎖により生成する。5,6,7,9,10日目の天気についても、4日目・8日目の天気にもとづいて同様に生成する。 3. 11日目の天気を1日目、4日目、8日目の天気から確率的に生成する。
これを学習できるか試してみましょう。
def _make_table() -> dict[str, list[float]]:
candidates = []
for i in range(1, 9):
for j in range(1, 9):
for k in range(1, 9):
if i + j + k == 10:
candidates.append((i, j, k))
table = {}
for i in WEATHERS:
for j in WEATHERS:
for k in WEATHERS:
table[i + j + k] = [p / 10 for p in _GEN.choice(candidates)]
return table
_ONE_FOUR_8_TABLE = _make_table()
def one_four_8(prev: str) -> str:
length = len(prev) // 2
if length == 10:
p = _ONE_FOUR_8_TABLE[prev[0: 2] + prev[6: 8] + prev[14: 16]]
return prev + _GEN.choice(WEATHERS, p=p)
elif length == 4 or length == 8:
return prev + _GEN.choice(WEATHERS, p=_MARKOV[""])
else:
return markov(prev)
generate(one_four_8, 11)'☀️☀️☀️🌧️🌧️🌧️🌧️☁️☁️🌧️☁️'こんな感じですね。では学習させましょう。さっきよりも少しデータが複雑なので、サンプルの数を増やしてみます。
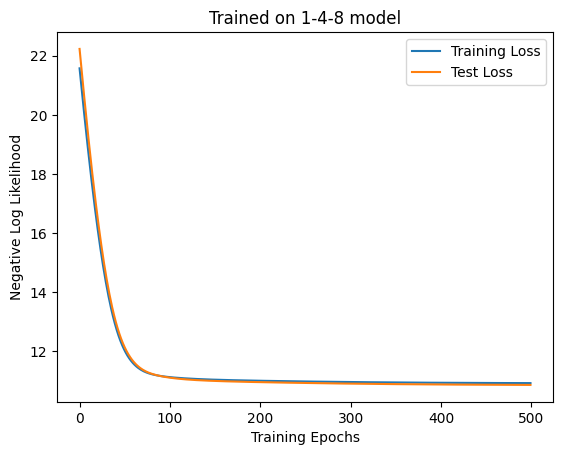
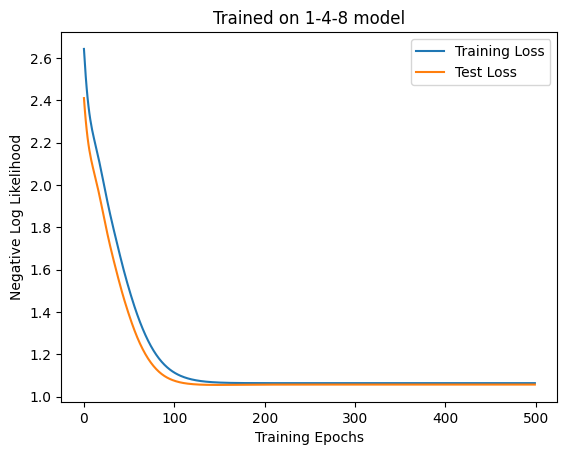
model = MaskedAttention(4, D_ATTN, 3, key)
ds = make_dataset(one_four_8, SEQ_LEN, 5000)
test_ds = make_dataset(one_four_8, SEQ_LEN, 1000)
model, key, loss_list, eval_list = train(500, 100, model, ds, test_ds, key, 1e-2)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on 1-4-8 model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))
visualize_attn(ax1, model, test_ds, 1)
visualize_attn(ax2, model, test_ds, 2)
f"Accuracy: {accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.3890000283718109'
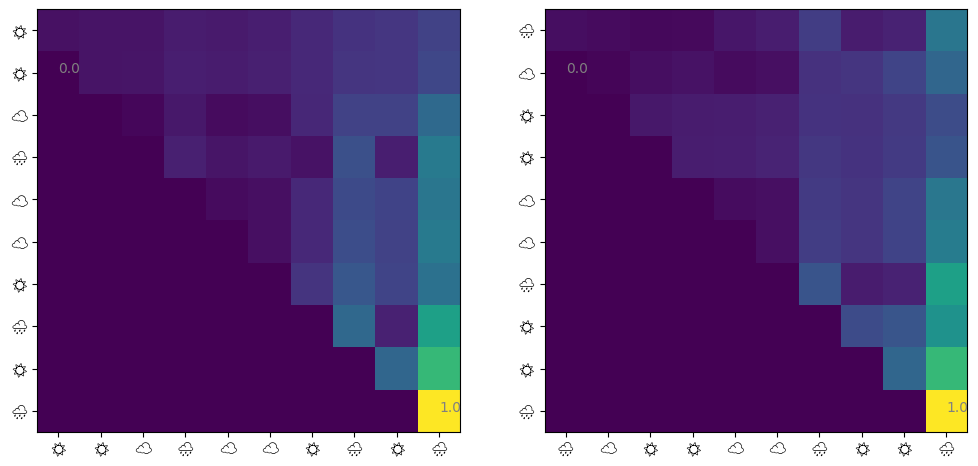
損失は小さくなっていますがAccuracyが悪くまたAttentionの出方も微妙ですね。一応1・48日目にも注意がいっていますが、先ほどの実験と同じく最後の日の注意が大きめに出ていますね。
勘のいい読者の方はお気づきかと思いますが、ここまで学習させた2つの天気列を表現するのに、self-attentionのような小難しいものはいらないですよね。最初のものは前日（10日目)の天気、次のやつは1・4・8日目から11日目の天気が決定されるため、入力された天気列の内部相関がタスクに一切関係ないからです。というわけで、線形モデル+ソフトマックス(いわゆるmultinomial logistic regressionというやつ)で学習してみましょう。
class LinearModel(eqx.Module):
w: jax.Array
b: jax.Array
def __init__(self, d_in: int, d_out: int, key: jax.Array) -> None:
w_key, b_key = jax.random.split(key)
self.w = jax.random.normal(w_key, (d_out, d_in))
self.b = jax.random.normal(b_key, (d_out,))
def __call__(self, seq: jax.Array) -> jax.Array:
return self.w @ seq.flatten() + self.b
def linear_neglogp(model: eqx.Module, seq: jax.Array, next_w: jax.Array) -> jax.Array:
logp = jax.nn.log_softmax(jax.vmap(model)(seq), axis=1) # B x OUT
logp_masked = logp * jax.nn.one_hot(next_w, num_classes=3)
return -jnp.mean(jnp.sum(logp_masked, axis=1))
model = LinearModel(4 * SEQ_LEN, 3, key)
model, key, loss_list, eval_list = train(
500, 100, model, ds, test_ds, key, 1e-2, linear_neglogp
)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on 1-4-8 model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
@jax.jit
def linear_accuracy(model: eqx.Module, seq: jax.Array, next_w: jax.Array) -> float:
tilde_v = jax.vmap(model)(seq) # B x OUT
inferred = jnp.argmax(tilde_v, axis=1)
n_correct = jnp.sum(inferred == next_w)
return n_correct / seq.shape[0]
f"Accuracy: {linear_accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.4230000078678131'
普通にこっちのほうが良さそうですね…。では、Attentionはどういう時に役に立つのでしょうか。
Attentionではパラメータの数が \((d_\textrm{in} + 1)(2d_\textrm{attn} + d_\textrm{out})\)になるのに対し、線形モデルでは\((d_\textrm{in}L + 1)d_\textrm{out}\)になることに注意しましょう。線形モデルではトークン列の長さに比例してパラメータの数が増えてしまいます。ただし、Attentionでは\(q^\top k\)を保持するのに\(O(L^2)\)のメモリ使用量が必要な点に注意が必要です。もっとも、Self-attention Does Not Need \(O(n^2)\) Memoryでは効率的な\(O(\sqrt{L})\)の実装が示されており、まあ何とかなるといえばなるようですが、それでも単純なRNNやCNNより遅くなります。
CNNやRNNと比べたとき、\(q^\top k\)により一層のレイヤーで任意のトークン間の依存関係が表現できるのはAttentionの利点と言えるでしょう。ただし\(q^\top k[i, j]\)は2つの埋め込み\(e[i], e[j]\)に対して線形な演算のみで得られるため、この2つの埋め込みが何か非線形な関数を介して依存している場合、その関係は一層のAttentionでは表現できません。
というわけで、一層の線形レイヤーと比較すると、パラメタ数が\(L\)に依存しないというメリットはあるものの、実際Attentionを使うともっと色々な関数が学習できるのかというとよくわかりません。もう少し試してみます。
以下の方法で天気列を生成します。過去\(n\)日間の天気を見て、🌧️の登場回数が\(k\)回なら、次の日の天気が🌧️になる確率を\(\frac{n - k}{2n}\)とします。☁️、☀️についても同様に確率を割り当てます。この方法で大量に天気列を生成して適当な部分列からデータセットを作ります。
from functools import partial
def ndays_model(prev: str, n: int = 10) -> str:
counts = np.zeros(3)
prev_n = prev[-2 * n: ]
for i in range(n):
prev_w_i = prev_n[i * 2: i * 2 + 2]
counts[WEATHERS.index(prev_w_i)] += 1
prob = (n - counts) / (n * 2)
return prev + _GEN.choice(WEATHERS, p=prob)
generate(ndays_model, 100, generate(markov, 10)) '☀️☀️☀️🌧️☀️☀️☁️☀️☁️☀️☀️🌧️☁️🌧️☁️☁️🌧️🌧️☁️☁️☀️🌧️☀️☀️☀️☀️☁️☁️🌧️🌧️🌧️🌧️🌧️☁️☀️☁️☀️☀️☀️☀️🌧️🌧️🌧️🌧️🌧️☀️☁️🌧️☁️☀️☀️☀️☁️☁️☀️🌧️☁️🌧️☁️☀️☀️☁️☁️☁️☁️☁️🌧️☁️🌧️☀️🌧️🌧️☀️☀️☁️🌧️☀️☀️🌧️☀️☁️☀️☀️☁️☁️☀️☀️🌧️🌧️🌧️☀️🌧️☁️🌧️🌧️☀️☀️🌧️☁️☀️🌧️🌧️☀️🌧️☀️☁️🌧️☀️☁️☁️'生成された天気列はこんな感じです。まず線形モデルを10日モデルで学習させます。この場合隠れ変数はありません。
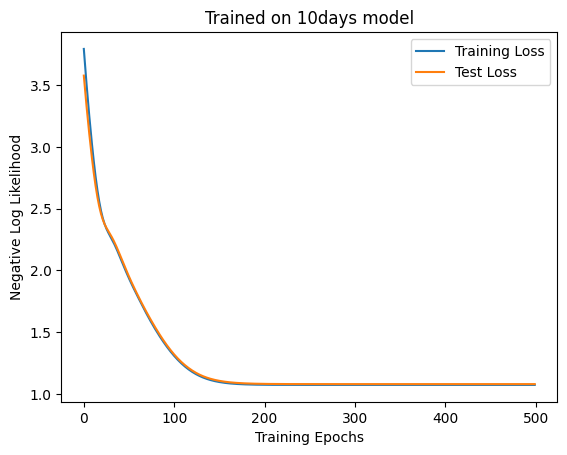
def make_ndays_dataset(seq_len, size, n: int = 10) -> Dataset:
weathers = generate(partial(ndays_model, n=n), seq_len * size * 2, generate(markov, n * 2))
w_list, e_list, nw_list = [], [], []
for _ in range(size):
start = _GEN.integers(0, seq_len * size * 2 - 11)
w = weathers[start * 2 : start * 2 + (seq_len + 1) * 2]
e = jnp.array(get_embedding(w[:-2]))
w_list.append(w)
e_list.append(e)
nw_list.append(WEATHERS.index(w[-2:]))
return Dataset(w_list, jnp.stack(e_list), jnp.array(nw_list))
ds = make_ndays_dataset(SEQ_LEN, 5000, n=10)
test_ds = make_ndays_dataset(SEQ_LEN, 1000, n=10)
model = LinearModel(4 * SEQ_LEN, 3, key)
model, key, loss_list, eval_list = train(
500, 100, model, ds, test_ds, key, 1e-2, linear_neglogp
)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on 10days model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
f"Accuracy: {linear_accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.3760000169277191'
次にSelf-Attentionを学習させます。
model = MaskedAttention(4, D_ATTN, 3, key)
model, key, loss_list, eval_list = train(500, 100, model, ds, test_ds, key, 1e-2)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on 10days model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))
visualize_attn(ax1, model, test_ds, 1)
visualize_attn(ax2, model, test_ds, 2)
f"Accuracy: {accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.3320000171661377'
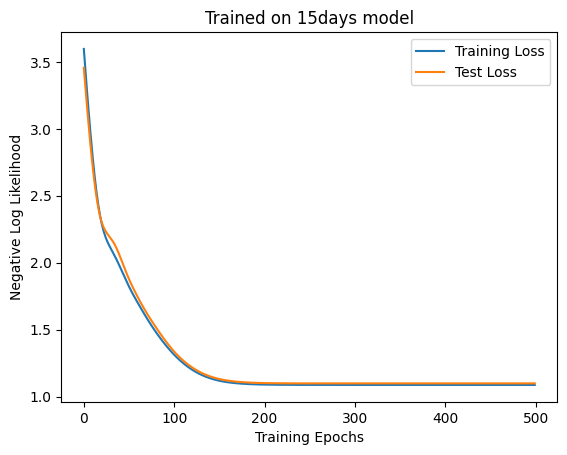
ほとんど変わりませんね。次に隠れ変数があるモデルとして、先程の10日モデルを15日モデルにしてみます。まず、線形モデルを学習させます。
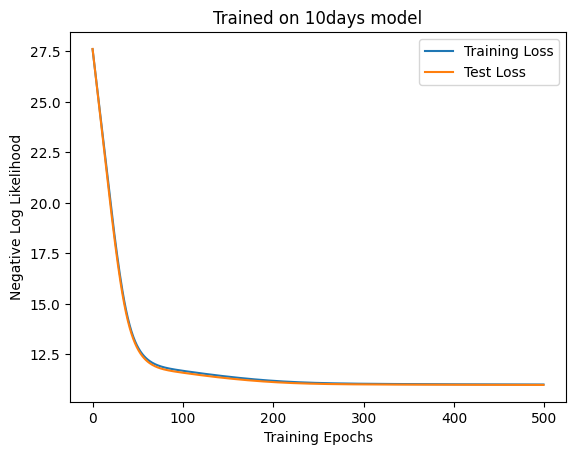
ds = make_ndays_dataset(SEQ_LEN, 5000, n=15)
test_ds = make_ndays_dataset(SEQ_LEN, 1000, n=15)
model = LinearModel(4 * SEQ_LEN, 3, key)
model, key, loss_list, eval_list = train(
500, 100, model, ds, test_ds, key, 1e-2, linear_neglogp
)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on 15days model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
f"Accuracy: {linear_accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.36900001764297485'
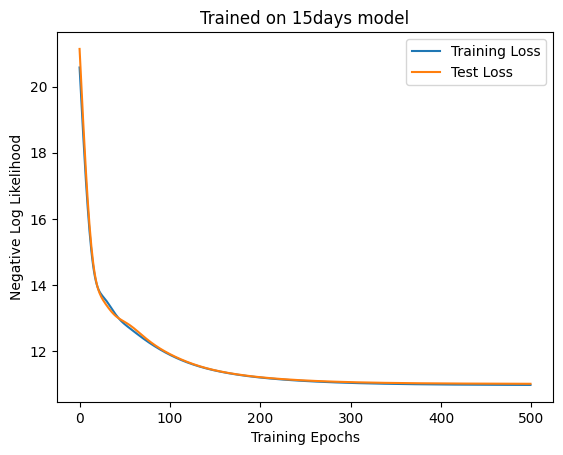
次にSelf-Attentionを学習させます。
model = MaskedAttention(4, D_ATTN, 3, key)
model, key, loss_list, eval_list = train(500, 100, model, ds, test_ds, key, 1e-2)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on 15days model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))
visualize_attn(ax1, model, test_ds, 1)
visualize_attn(ax2, model, test_ds, 2)
f"Accuracy: {accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.3140000104904175'
この場合も結局Self-Attentionのほうが悪くなってしまいました。悲しい。
隠れ変数があっても線形モデルの方が性能がいいということは、たぶん線形で解けるタスクではどうあがいても線形モデルに勝てないということなのでしょう。なのでもっと難しいデータを考えます。 10日ぶんの天気列の🌧️、☁️、☀️にそれぞれ0, 1, 2を割り当てて作ったベクトルを\(y\)とします。また、\(\beta = (0, 1, 2, 3, 2, 1, 0, 1, 2, 3)^\top\)とします。このとき、次の日の天気を\((y(2 - y)\cdot \beta) \mod 3\)とします。これだと芸がないので一応他の天気も2%くらいの確率で出るようにしておきます。
_BETA = np.tile([0, 1, 2, 3, 2, 1], (10,))
def dotmod_model(prev: str, n: int =10) -> str:
y = np.zeros(n, dtype=int)
prev_n = prev[-2 * n:]
for i in range(n):
prev_w_i = prev_n[i * 2: i * 2 + 2]
y[i] = WEATHERS.index(prev_w_i) + 1
prob = [0.02, 0.02, 0.02]
prob[np.dot(y * (2 - y), _BETA[: n]) % 3] = 0.96
return prev + _GEN.choice(WEATHERS, p=prob)
def make_dotmod_dataset(seq_len, size, n: int = 10) -> Dataset:
weathers = generate(partial(dotmod_model, n=n), seq_len * size * 2, generate(markov, n * 2))
w_list, e_list, nw_list = [], [], []
for _ in range(size):
start = _GEN.integers(0, seq_len * size * 2 - 11)
w = weathers[start * 2 : start * 2 + (seq_len + 1) * 2]
e = jnp.array(get_embedding(w[:-2]))
w_list.append(w)
e_list.append(e)
nw_list.append(WEATHERS.index(w[-2:]))
return Dataset(w_list, jnp.stack(e_list), jnp.array(nw_list))
generate(dotmod_model, 100, generate(markov, 10))'🌧️🌧️☁️☁️☁️☀️🌧️🌧️☁️☀️☀️☁️🌧️☀️☁️☁️☁️☁️☀️🌧️☀️🌧️☁️☀️☀️☀️☁️☁️☁️☀️☁️🌧️🌧️☀️🌧️☁️🌧️☁️☁️☁️☀️☀️☁️☁️☀️☁️🌧️🌧️☀️🌧️☁️🌧️☁️☁️☁️☁️☀️☁️☁️☀️☁️🌧️🌧️☀️🌧️☁️🌧️☁️☁️☁️☀️☀️☁️☁️☀️☁️🌧️🌧️☀️🌧️☁️🌧️☁️☁️🌧️☀️☁️☀️☁️🌧️🌧️☀️☀️☀️☁️🌧️☀️☁️☁️☁️☁️☀️🌧️☀️☀️☁️🌧️☁️☁️☁️'ぱっと見ではまるで法則性がわからない天気列が生成できました。これを学習させてみましょう。まずは線形モデルです。
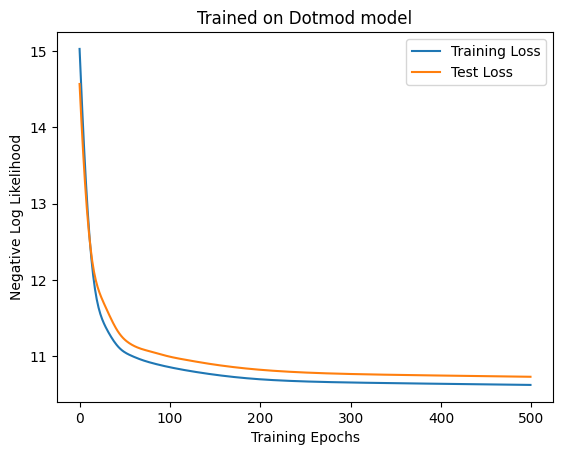
ds = make_dotmod_dataset(SEQ_LEN, 5000)
test_ds = make_dotmod_dataset(SEQ_LEN, 1000)
model = LinearModel(4 * SEQ_LEN, 3, key)
model, key, loss_list, eval_list = train(
500, 100, model, ds, test_ds, key, 1e-2, linear_neglogp
)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on Dotmod model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
f"Accuracy: {linear_accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.6990000605583191'
意外に7割近く正解していますね。次にSelf-Attentionを学習してみます。
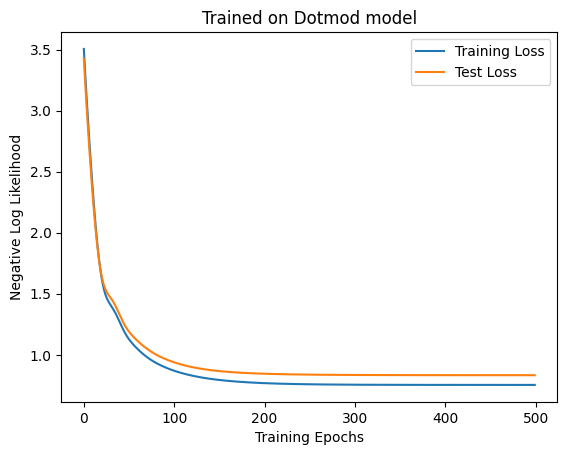
model = MaskedAttention(4, D_ATTN, 3, key)
model, key, loss_list, eval_list = train(500, 100, model, ds, test_ds, key, 1e-2)
plt.plot(loss_list, label="Training Loss")
plt.plot(eval_list, label="Test Loss")
plt.title("Trained on Dotmod model")
plt.xlabel("Training Epochs")
plt.ylabel("Negative Log Likelihood")
plt.legend()
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 6))
visualize_attn(ax1, model, test_ds, 1)
visualize_attn(ax2, model, test_ds, 2)
f"Accuracy: {accuracy(model, test_ds.embeddings, test_ds.next_weather_indices).item()}"'Accuracy: 0.4480000138282776'
またしてもSelf-Attentionのほうがだめという結果になりました。
このブログ記事では、Transformerの構成要素であるMultihead Attentionの簡略版であるSingle Attentionについて何をしているのか概観し、いくつか簡単なデータセットでの学習を試みました。結局全タスクで線形関数以下の性能に終わってしまい、メモリ使用量以外のメリットが見えてこなかったというのが正直なところです。MLPも例のscaling lawでスケールするんじゃないかと思えるほどです。表現力という点ではスケールはするんでしょうが。 今後のブログでは、
などもやってみようと思います。